提桶跑路笔记

408计组——2.数据的表示和运算

数制与编码

进位计数制及其相互转换

  • 计算机采用二进制的原因

    1. 二进制编码、运算规则简单，逻辑门电路能实现算术运算
    2. 使用两个稳定状态的物理器件即可以表示二进制
    3. 真假与 10 对应，为逻辑判断提供便利

进位计数法

  • 基数

    每个数位用到的不同数码个数，十进制基数 10（0~9 数码）

  • 位权

    进位数每个数位所占真实数值的权重

    进位数数值大小即为各位数码按权相加

  • r 进制数

    $K_nK_{n-1}…K_0K_{-1}…K_{-m}$

    r 进制数的 10 进制数值表示为：

    $K_nr^n+K_{n-1}r^{n-1}+\cdots+K_0r^0+K_{-1}r^{-1}+\cdots+K_{-m}r^{-m}=\sum_{i=n}^{-m}K_ir^i$

    其中 r 为基数，ri 为第 i 位的位权，Ki 为任意数码

    即**数位的数字 x 该位位权 求和**

  1. 十进制（D，Decimal system）

  2. 二进制（B，Binary）

    基数为 2，数位位权为 2i，i 为位数

  3. 八进制（O，Octal number system）

    基数为 8，3 位 2 进制数码为 1 组即 1 位 8 进制数码

  4. 十六进制（H，Hexadecimal）

    基数 16，数码 0~9+A~F，4 位 2 进制数码为 1 组即 1 位 16 进制数码

进制转换

  1. B 转 O、B 转 H

    (1 111 000 010.011 01)2

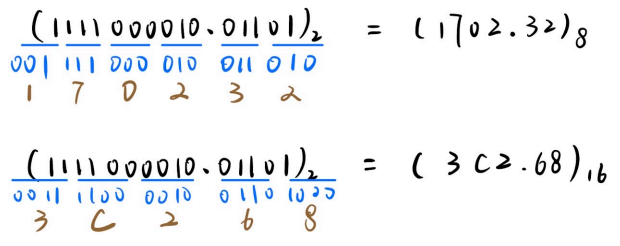
    ​image​

    以小数点分界，8 进制 3 位 1 组，按权相加后结果即 1 位 8 进制数

    二进制 010​ 转换为八进制： $0 \times 2^2 + 1 \times 2^1 + 0 \times 2^0 = 4 + 0 + 1 = 2$

    其他位同理，十六进制按 4 位一组同理

  2. 任意进制转十进制

    即 r进制数的十进制表示

  3. 十进制转任意进制

    • 整数部分除基取余法

      先取得的余数为最低位，商为 0 时结束

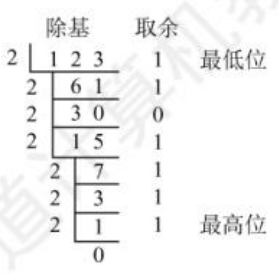
      ​image​

    • 小数部分乘积取整法

      取小数部分乘进制，取整数，先取得为高位，直到乘积为 1.0

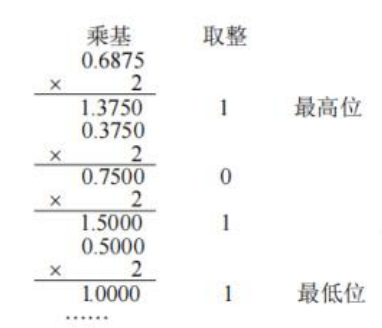
      ​image​

      应注意并非所有十进制小数都可以准确使用二进制表示如 0.3

      任意二进制小数都能使用十进制表示

无符号数

均为数值位，没有符号位

n 位二进制数表示范围：0~2n-1

unsigned int，没有无符号小数

有符号数

真值和机器数

  • 真值：+5，-5

  • 机器数：05,15

    通常使用 0 表示正，1 表示负，将符号数字化的数称为机器数

原码

  • 定点整数

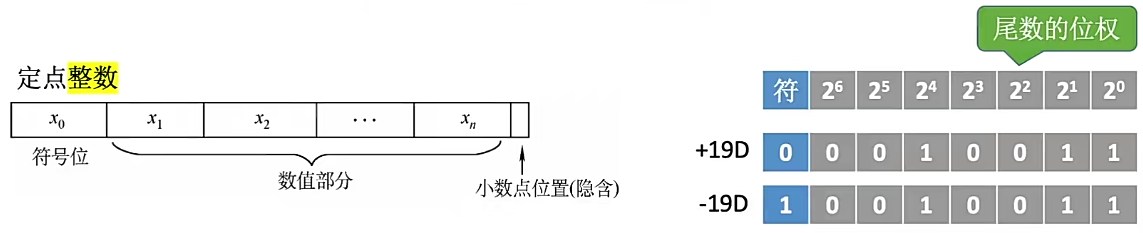
    ​image​

  • 定点小数

    ​image​

设字长为 n+1，表示位不足补 0

原码整数范围 $-(2^n-1)\leq x\leq2^n-1$
一共可以表示 $2^{n+1}-1$ 个数
范围-1是因为正数负数各去掉一个0，总数-1是因为0有两个表示

原码小数范围 $-(1-2^{-n})\leq x\leq1-2^{-n}$

0 有两个 +0 和-0

  • 优点

    1. 与真值对应关系简单直观
    2. 原码乘除运算简便

  • 缺点

    1. 0 的表示不唯一
    2. 加减运算复杂

反码

符号位为 0，与原码一致

符号位为 1，数值位取反

表示范围与原码一致，无实际作用

补码

正数补码 = 原码

负数原码 转 补码——数值位取反 +1

负数补码 转 原码——数值位取反 +1

补码取相反数——全部取反 +1

​image​

$\begin{aligned} & [+0]{\text{原}}{=00000000} & & [-0]{\text{原}}{=10000000}\ & [+0]{\text{反}}{=00000000} & & [-0]{\text{反}}{=11111111}\ & [+0]_{补}{=00000000} & & \end{aligned}$

补码真值 0 只有一个00000000
多余一个二进制表示1,0000000，规定用于表示最小负数：

  • 定点整数

    表示真值​ -2​**n**

    $-(2^{n})\leq x\leq2^{n}-1$

  • 定点小数

    表示真值​ -1

    $-1\leq x\leq1-2^{-n}$

  • 补码表示有符号整数优势

    1. 0 的补码表示唯一
    2. 补码运算规则简单，符号位参与二进制计算
    3. 多表示一个最小负数

  • 补码比较大小

    • 正数，和原码相同

    • 负数，数值位原码规则越大的，补码真实值越小

      -32：补码：1，100000
      大于-32的负数,补码应该在数值位上比100000大，如1，100001

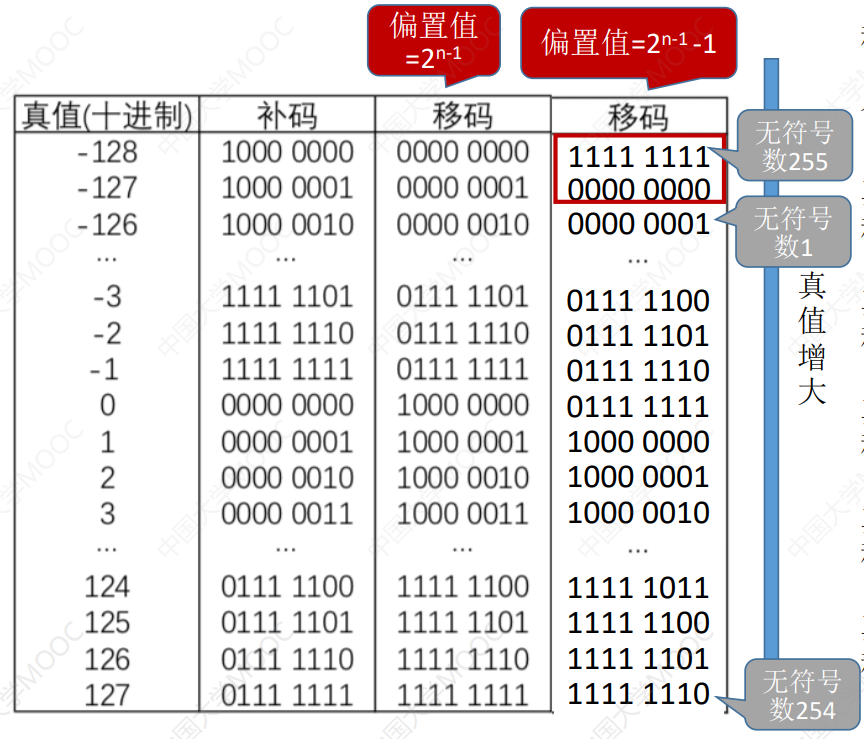
移码

只能表示整数

移码=真值 - 偏置值，本例中偏置值取 2​n-1，在 IEEE754 标准中取 2​n-1​ -1

将二进制视为原码，偏置值原码规则转换二进制相减，原码转换即可

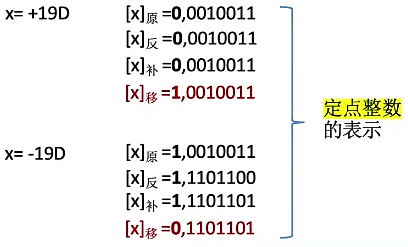
​image​

  • 移码保持了数据原有的大小顺序，真值大移码大
  • 移码只有一个零表示
  • 和补码一样多表示一个最小负数

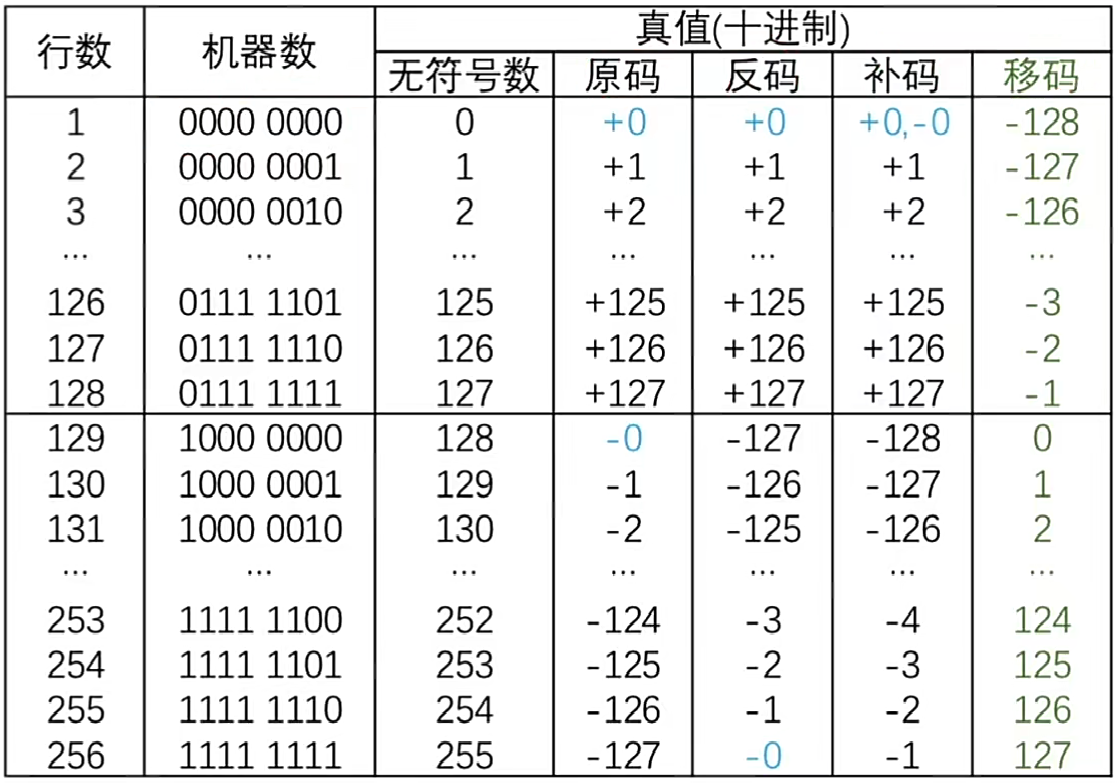
​image​

相互转换

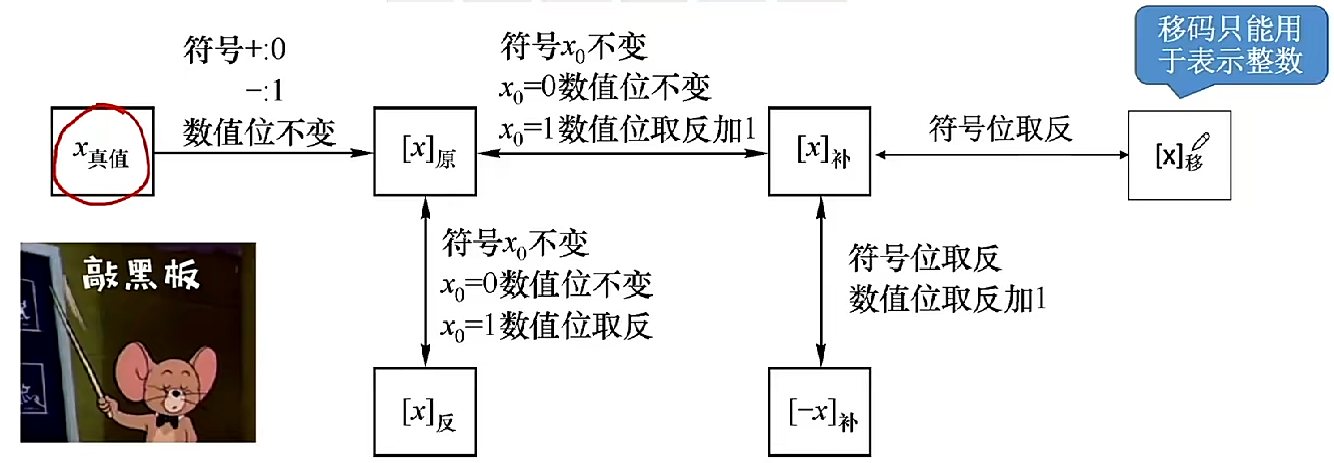
​image​

C 语言中整数类型及类型转换

C 语言整型数据类型

  • 字符型

    ​char​，8 位

  • 短整型

    ​short​、short int​，16 位

  • 整型

    ​int​，32 位

  • 长整型

    ​long​、long int​，由机器位数决定

​char ​默认为有符号整数，其他默认无符号整数（unsigned​）

整型数据按补码形式存储，​unsigned​ 最高位为​数值位​，​​signed​ 为​符号位

有符号数无符号数转换

改变解释位的方式

  • ​short ​转 unsigned short​

    short x=-4321;
unsigned short y=(unsigned short)x;//y=61215

    ​image​

    第 15 位由符号位变为数值位

同时存在无符号数与有符号数参与运算时，规定按无符号数计算

不同字长整数转换

  • 大字长转小字长

    高舍去，低复制

  • 小字长转大字长

    低位位值保持小字长不变，高位位值填充：

    • 原数字无符号整数： 高位位值填充 0

    • 原数字有符号整数：高位位值填充原数字符号位

      short x = -4321
int y = x
//x=y=-4321
x的补码为                    1110 1111 0001 1111
y的补码为1111 1111 1111 1111 1110 1111 0001 1111
y高位填充符号位

      short x = -4321
unsigned short u = (unsigned short)x
//x=-4321 u=61215
x的补码为1110 1111 0001 1111
u的补码为1110 1111 0001 1111
x的最高位由符号位变为数值位，真值变大

      unsigned short u = 61215
unsigned int v = u
//x=61215 u=61215
x的补码为                    1110 1111 0001 1111
u的补码为0000 0000 0000 0000 1110 1111 0001 1111
无符号进行零扩展，填充0

数据的存储和排列

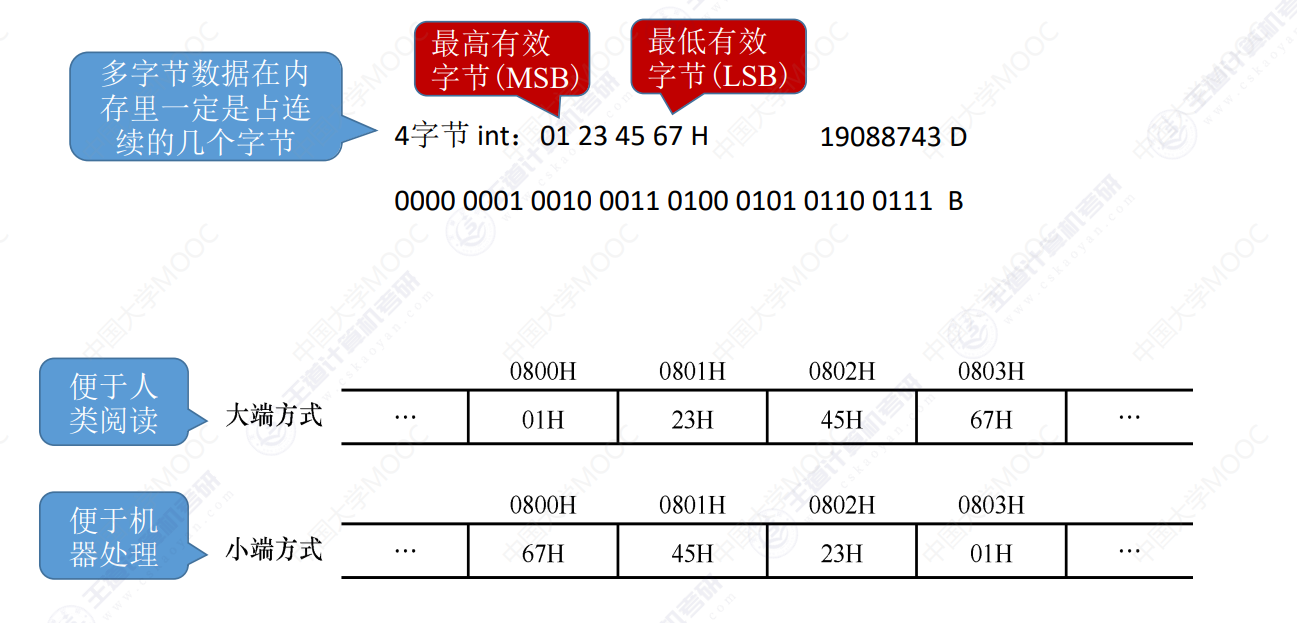
大小端方式存储

计算机在存储多字节数据时的字节顺序

  • 大端方式：个位在高位内存（按人类习惯）
  • 小端方式：个位在低位内存

读取时，只需要读取最低位即可，未指明读取位数即默认为读取到的寄存器的位数

​image​

对齐方式存储

计算机按字节编址，一个字节对应一个地址，题目中具体使用编址方式按题目分析

下例中字长为4B，即16位机器字长

  • 边界对齐

    浪费部分空间，读取速度快

    ​image​

    int：32位，char：8位，float：16位，按边界对齐存储时，int占一行，char和float同行，char后空一个字节以便于对齐（填充）

  • 边界不对齐

    空间利用率高，读取速度慢

    ​image​

存储单位

  • 字节（B，Byte）

    数据处理的基本单位

    一个字节由 8 个二进制位构成，即 1 个字节等于 8 个比特（1 Byte = 8 bit）

  • 字

    字的长度即字长，与计算架构有关，比如32位机，一个字就是32位，4B

    机器字长

    32 位电脑，32 即机器字长，简称字长

    计算机进⾏⼀次整数运算所能处理的⼆进制的位数

    通常与 CPU 寄存器位数、ALU 有关

    字长越长，数表示范围越大，字长常为 8 的整数倍

  • 比特（b，bit）

    计算机内部数据存储的最小单位

    每个比特都由“0”和“1”表示

    11010100 是一个 8 位二进制数，其中每一位都是一个比特

运算电路

数电基础

逻辑门电路

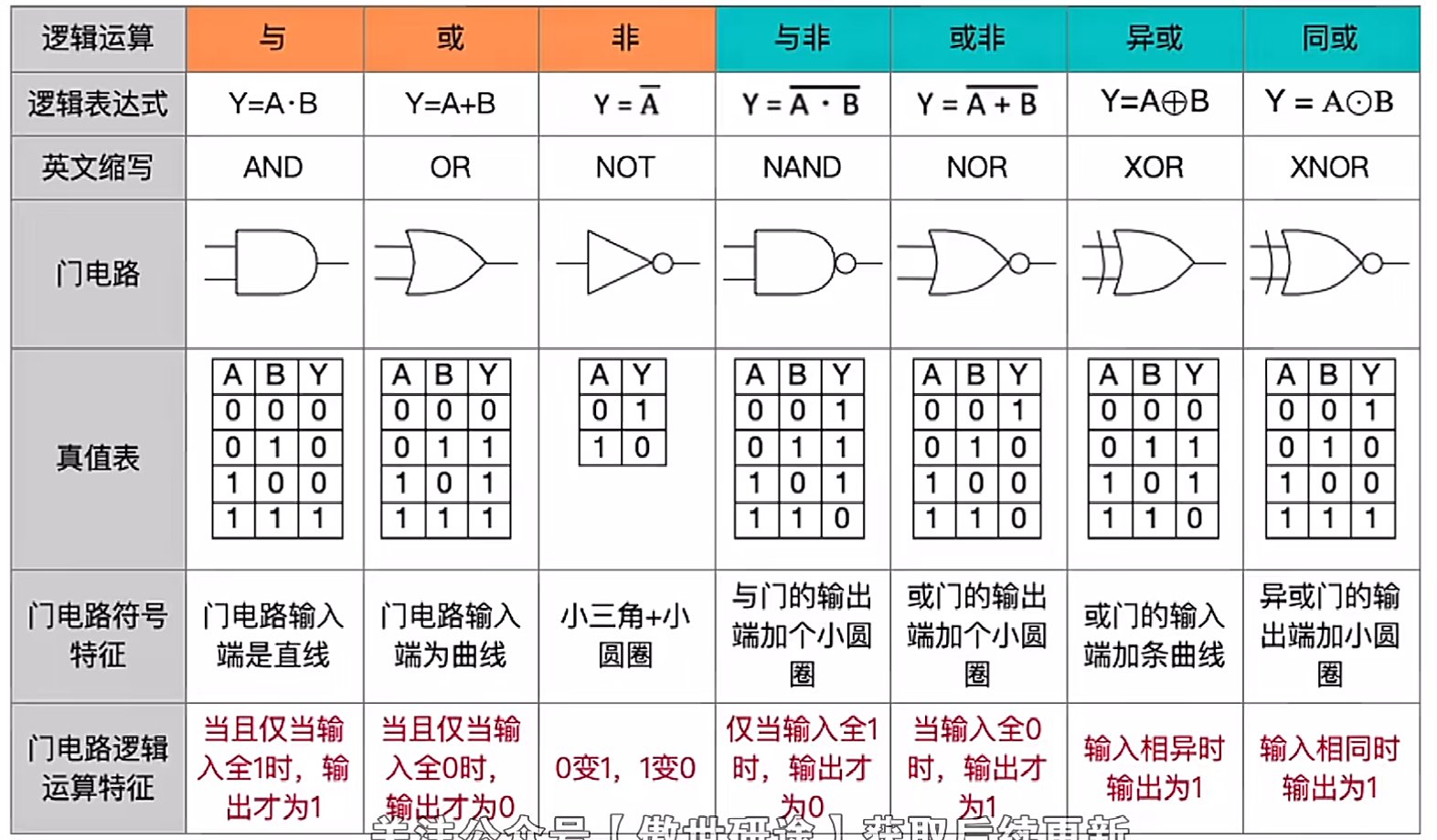
​image​

多路选择器（MUX，multiplexer）

多输入中选择一个输入通过 MUX

使用控制信号 op 控制输入，k 个输入的控制信号位数为 $\mathrm{m}\geq[\log_{2}k] bit$

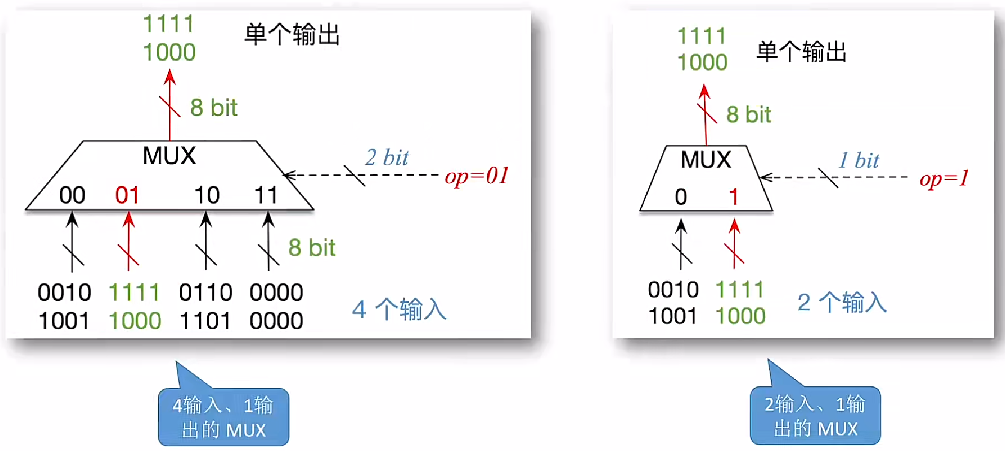
​image​

当预留一个信号用于阻止所有输入时，$\mathrm{m}\geq[\log_{2}k+1] bit$

三态门

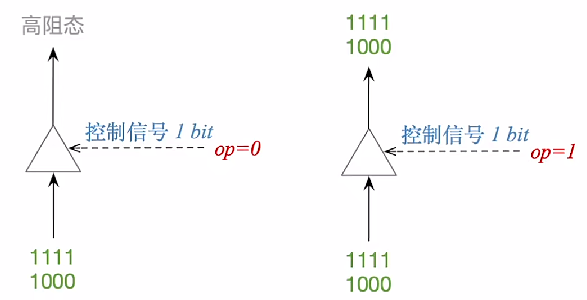
​image​

控制单线数据是否能够通过

基本运算部件

加法器

一位全加器（FA）

最基本加法单元，支持 1 位的加法运算

  • 实现

    1. 本位和：$\mathrm{S_i}=\mathrm{A_i}\oplus\mathrm{B_i}\oplus\mathrm{C_i}$
    2. 高位进位：$C_i=A_i B_i+(A_i\oplus B_i) C_{i-1}$
并行加法器

  • 串行进位

    n 个 FA 相连得到 n 位加法器，支持 n 位并行加

    进位信息串行产生，速度慢

  • 并行进位

    在串行进位基础上优化增加 CLA（超前进位部件）

    进位信息并行产生，速度快，相互进位没有依赖关系

带标志位加法器

能够进行有符号整数加减运算，标志存储于psw程序状态字寄存器中

  • OF（Over Flag）溢出标志

    判断带符号​数运算是否溢出，1 溢出

    $OF=C_{n}\oplus C_{n-1}$

  • SF（Sign FLag）符号标志

    判断运算结果正负性，1 为负

    $SF$=补码运算结果最高位

  • ZF（Zero Flag）零标志

    判断结果是否为零,1 为零

    $ZF=\overline{S_{n}+\cdots+S_{2}+S_{1}}$

  • CF（Carry Flag）进位/借位标志

    判断无符号​数运算是否溢出，1 溢出

    $CF=C_{\mathrm{out}}^{}\oplus C_{\mathrm{in}}^{}=C_{\mathrm{n}}^{}\oplus C_0$

算术逻辑单元（ALU）

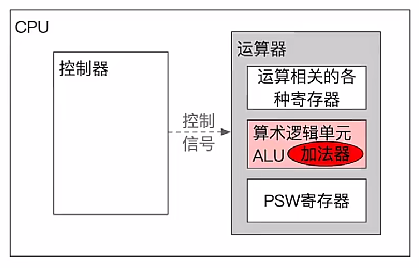
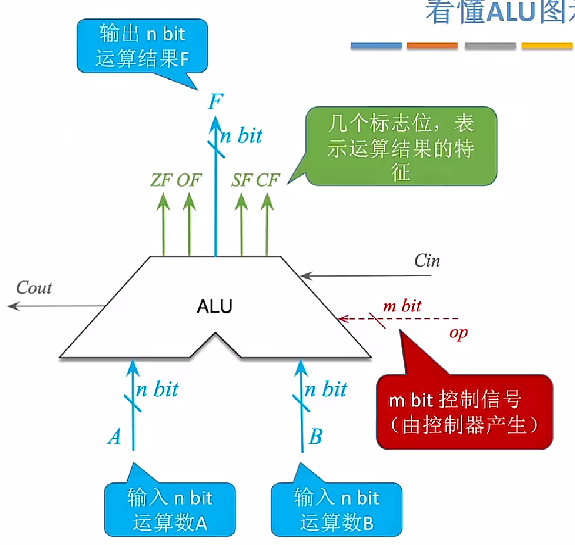
​image​

​image​

  • CPU 的核心是 ALU，ALU 的核心是​加法器，ALU 主要进行算术运算和逻辑运算
  • ALUop 发出控制信号决定 ALU 的处理操作，支持 k 种功能，则控制信号位数 $\mathrm{m}\geq[\log_{2}k] bit$
  • 发出控制信号后，由一个 MUX 选择输出某种操作结果
  • ALU 的运算位数决定了计算机的机器字长
  • 标志位表示运算结果特征，送入 PSW 程序状态字寄存器中保存（FR 标志寄存器）
  • ALU进行加法运算时，必须同时输入两个数

定点数的表示和运算

定点数的移位运算

算术移位

原码符号位不变

码 添补
正数 原、补、反 0
负数 原码 0
补码 左移 0
右移 1
反码 1

  • 原码的算术移位

    符号位不变​，数值位整体移动

    • 右移

      高位补 0，低位舍弃

      舍弃 0​，相当于 ÷2；舍弃 1​，则丢失精度

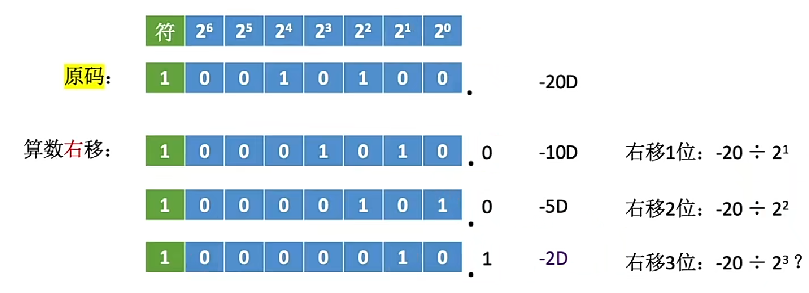
      ​image​

      即图中最右侧 1 移位后其位权为 2​ -1​ ，被舍弃，丢失 1/2

    • 左移

      低位补 0，高位舍弃

      **舍弃 0​，相当于 x2；​舍弃 1**​，产生严重误差

      和右移同理，高位舍弃 1 的位权过大，故误差严重

  • 反码算术移位

    • 正数与原码相同
    • 负数补位使用 1，其他相同

  • 补码​算术移位

    • 正数与原码相同

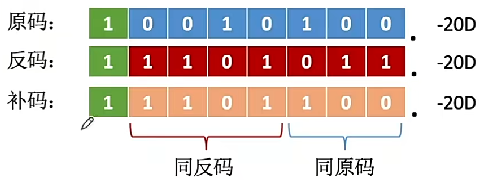
    • 负数

      • 右移（同反码）：高位补 1，低位舍弃
      • 左移（同原码）：低位补 0，高位舍弃

      ​image​

逻辑移位

视为无符号数移位

左移，低位补 0

右移，高位补 0

循环移位

  • 不带进位位

    首尾相接移位

  • 带进位位

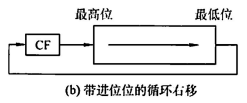
    ​image​

定点数加减运算

原码加减

同号加法，绝对值相加，符号不变
异号加法，绝对值大-小，符号取大者

减法运算将 “减数” 取反转为加法

补码加减

符号位和数值位一起运算
溢出高位舍弃

补码减法转变为加法进行运算

补码加法溢出判断

异号补码加减不会溢出

  • 上溢

    结果超过 +127

    正 + 正 = 负

  • 下溢

    结果小于-128

    负 + 负=正

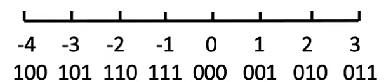
​image​

如三位补码，当计算 2+2 时，0,10 + 0,10 = 1,00（2+2=-4，正+正=负）
即从 2 开始沿数轴移动两格得到-4

补码加法溢出机器判断

符号位发生改变即溢出

  1. 一位符号法

    依据正 + 正=负以及负 + 负=正判断

    $V=A_{\mathrm{S}}B_{\mathrm{S}}\overline{S_{\mathrm{S}}}+\overline{A_{\mathrm{S}}}\overline{B_{\mathrm{S}}}S_{\mathrm{S}}$

    V=0，无溢出

    V=1，溢出

  2. 一位符号由数据位进位情况判断

    符号位进位、最高数值位进位，异或判断

    上溢：0、1

    下溢：1、0

  3. 双符号位法（模 4 补码）

    正数为 00，负数为 11

    当两位数不同时发生溢出，异或判断

    此时第一位正确正负性，第二位错误正负性

    上溢：01

    下溢：10

    双符号位只有在计算时复制一位符号，存储时不会增加占用

补码加减机器运算原理

直接相加，溢出舍弃

减法转换为加法，减数取相反数

转换原理：

8 位二进制数，其表示范围为 0~255

两个 8 位二进制数相加，超过 8 位的部分将被硬件舍弃，也即对原结果进行了 %2​8

1011 1100 (188)10 +
0100 0110 (70)10 =
1 0000 0010 (258)10 舍去溢出 1，即原结果
0000 0010 (2)​10 即结果为 2，258 % 2​8 = 2

合理利用溢出舍去的特性，可以将减法变为加法

十进制下，188 - 80 = 108 在模 28 意义下转为加法
( 188 + 176 )% 256 = 108

利用硬件计算加法的自然溢出即可将减法转变为加法

1011 1100 - 1011 1100 +
0101 0000 = 取反+1得 1011 0000 =
0110 1100 1 0110 1100

80 + 176 = 256 转变方法即将“减数”的全部位取反 +1

0101 0000 取反
1010 1111 +1=
1011 0000

​#408考点#​
问：有符号整数加减与无符号整数加减使用同一电路运算的理由

答：

n 位加法器实现的是 %2n 无符号整数加法运算

对于无符号整数a 和 b

a+b 可以直接用加法器实现
a-b 即 a-b= a+[-b]补（%2n)

所以 n 位无符号整数加减运算可在 n 位加法器中实现

对于有符号整数a 和 b

用补码表示，补码加减运算公式为：

[a+b]补=[a]补 +[b]补（%2n)
[a-b]补=[a]补 +[-b]补（%2n)

所以 n 位有符号整数加减运算可在 n 位加法器中实现

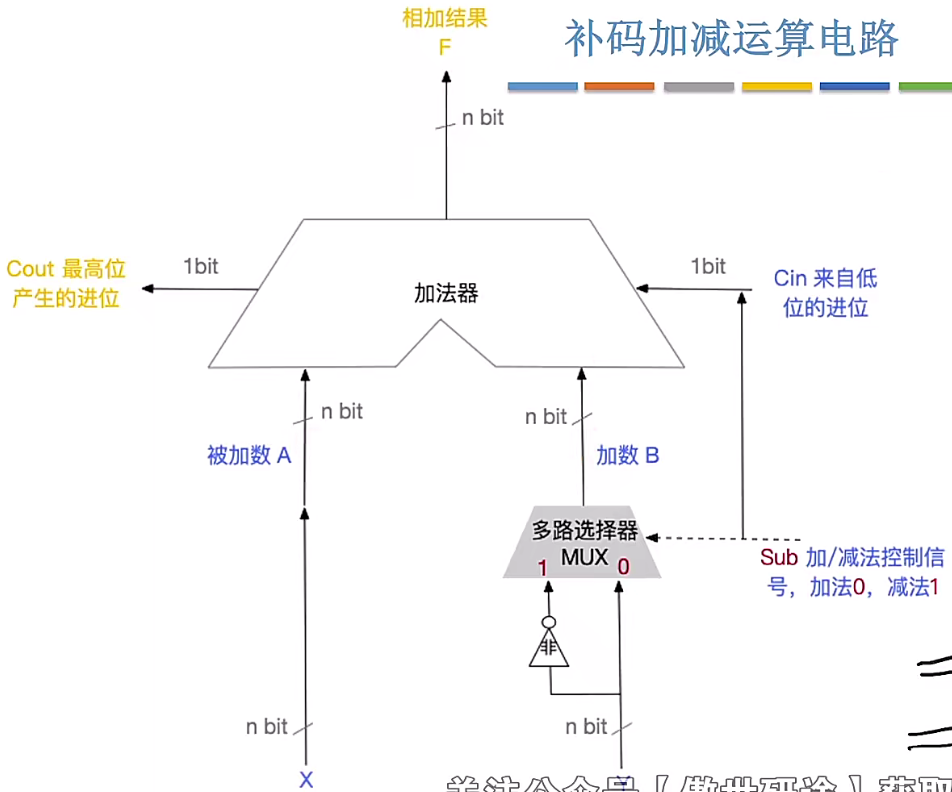
​image​

减数 “取反加一”，在电路中为两步操作

通过多路选择器 + 非运算电路，MUX同时输入原值与取反值

Sub信号控制加减法，同时传入MUX与Cin
MUX 收到 1 取反值进入
Cin 的 1 视为进位加入取反值

即实现取反加一

定点数乘除运算

考题中，常使用乘除运算考察移位与数据表示范围
一般不考察原理

乘法运算基本原理

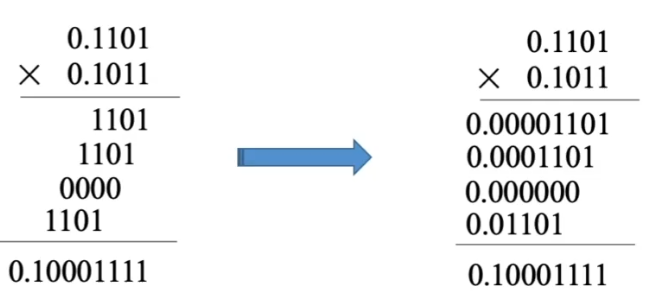
0.1101 × 0.1011

(被乘数) $0.1101=1101\times2^{-4}$

(乘数) $0.1011=1\times2^{-1}+0\times2^{-2}+1\times2^{-3}+1\times2^{-4}$

$0.1101\times0.1011=(1101\times1\times{\color{Red} 2^{-8}} )+(1101\times1\times{\color{Red} 2^{-7}} )+(1101\times0\times{\color{Red} 2^{-6}} )+(1101\times1\times{\color{Red} 2^{-5}} )$

​image​

​#408考点#​

问：为什么计算机没有乘法指令也能进行乘法运算

答：乘法可以转换为加法和移位的循环运算

原码一位乘法

  • 符号位与数值位分开计算
  • 乘积符号 = 两数符号位异或（同号正，异号负）
  • 乘积数值 = 两数绝对值相乘

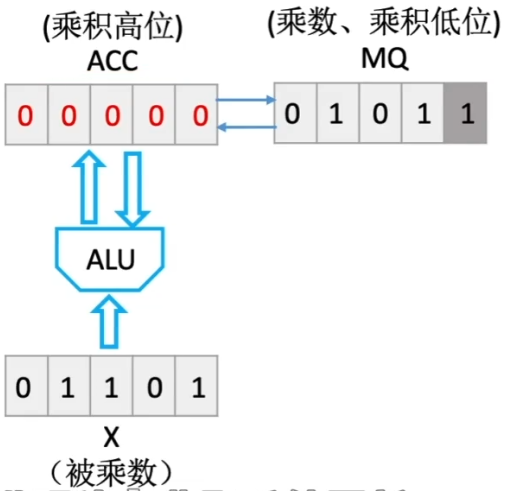
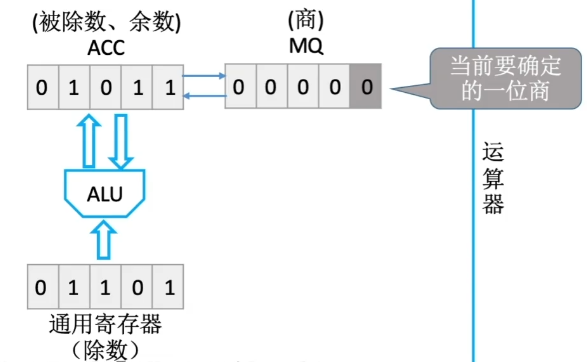
初始运算器存储如下所示

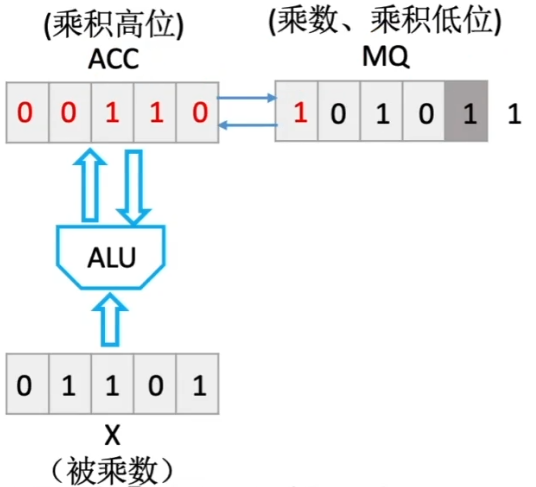
​image​

​image​

​image​

  • MQ 灰色为当前参与运算的位

    • 若为 1，ACC 加被乘数
    • 若为 0，ACC 加 0

  • ACC 加和后，ACC 与 MQ 整体右移一位（逻辑移位）

    如图二，此时灰色部分 1 即为乘数第二个参与运算的数字

    即对应手算中第二步错位加法

    001101 +

    01101

  • 重复运算步骤

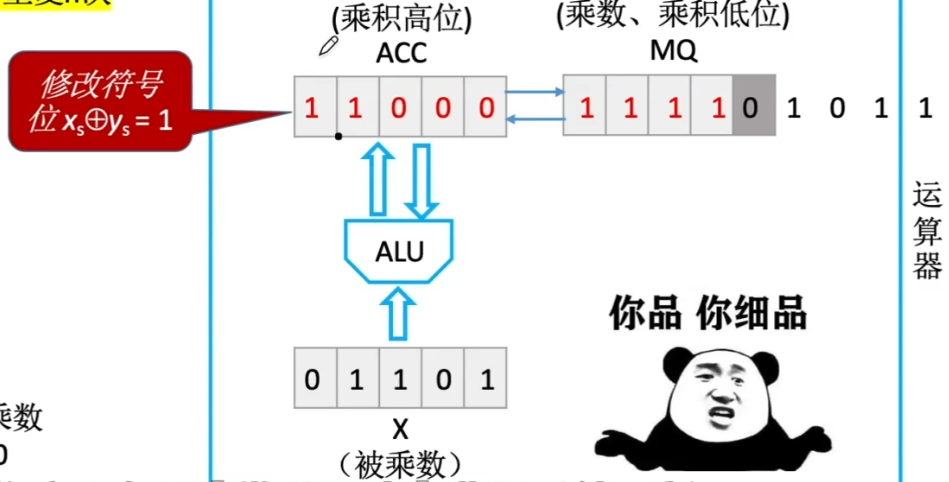
​image​

补码一位乘法

  • 与原码一位乘法对比

    1. MQ 中最低位为辅助位，其上一位为当前计算位

    2. MQ 多一辅助位，因此 ACC、X 均多一位，采用双符号位

    3. 进行加法运算时，辅助位-计算位=

      • 1，ACC + X 补码
      • 0，ACC + 0
      • -1，ACC + -X 补码

    4. 移位使用补码算术右移

    5. 符号位参与计算

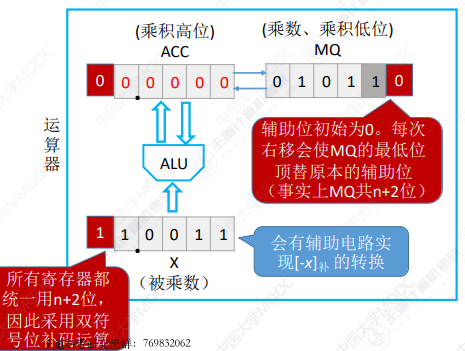
​image​

除法运算基本原理

x ÷ y = a…b ——> x = ay + b

0.211 ÷ 0.985 = 0.214…0.00021

(除数 y) $0.214=2\times10^{-1}+1\times10^{-2}+4\times10^{-3}$

(商 a) $0.985=985\times10^{-3}$

$a\times y=0.985\times0.214=(985\times2\times10^{-4})+(985\times1\times10^{-5})+(985\times4\times10^{-6})=0.21079\\qquad\qquad\qquad\qquad\qquad=0.1970\qquad\qquad+0.00985\qquad\qquad+0.00394$

即商的位拆分逐个乘除数，尽可能匹配上一步剩余的余数

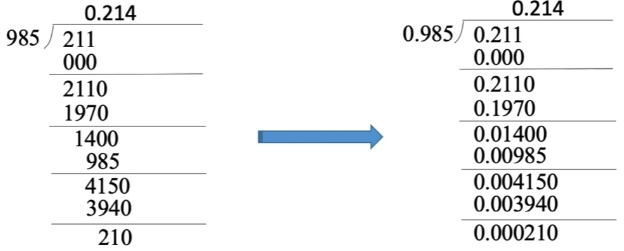
​image​

原码除法——恢复余数法

  • 符号位与数值位分开计算
  • 商符号 = 两数符号位异或（同号正，异号负）
  • 商数值 = 两数绝对值除法

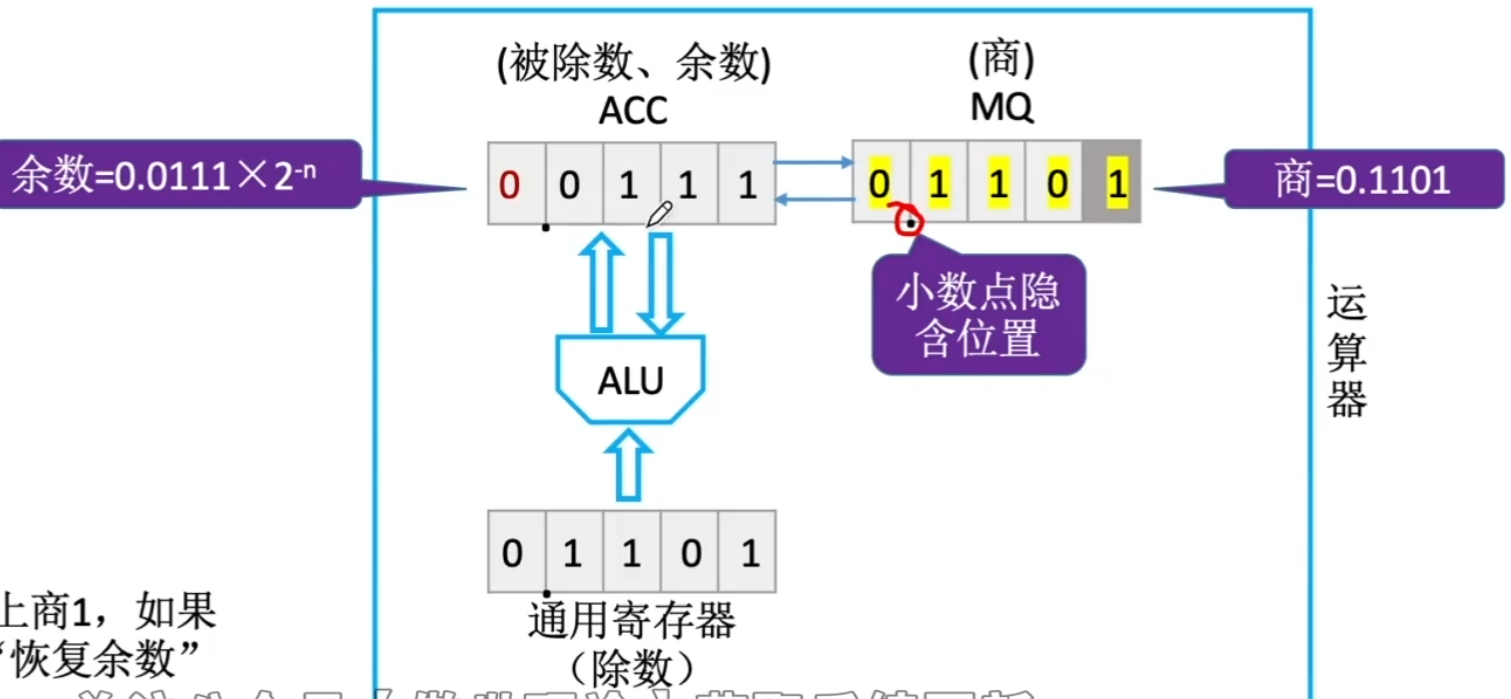
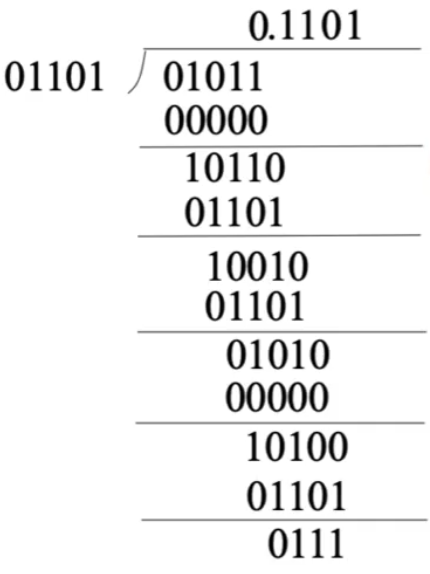
​image​

​image​

​image​

  1. x÷y

  2. ACC÷X，计算机首先尝试商 1，即灰色位为 1

    ACC-=[y]补 = ACC+=[-y]补

    • 若结果为正，进行 3.

    • 若结果为负

      ACC+=[y]补，将 ACC 恢复为商 0 结果，灰色位 0，进行 3.

  3. ACC 与 MQ 整体“算术左移”，重复 2.

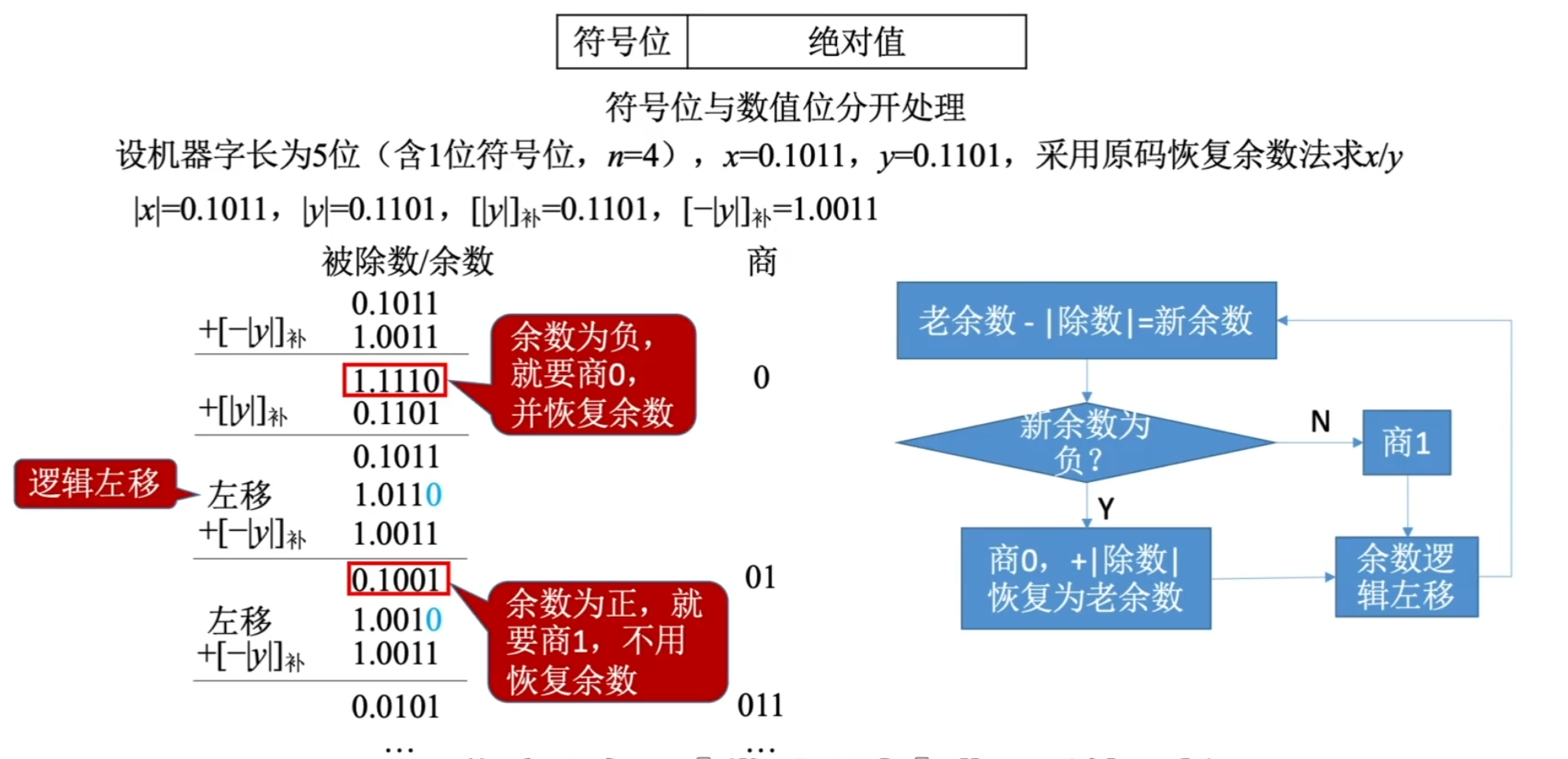
​image​

手算时，若商 1 时余数为负数，改为商 0，将该​负数余数左移 1 位 + 余数​即可得到下一步余数

原码除法——加减交替法

​image​

符号位最后异或得到

定点小数无法表示大于 1 的数，因此规定定点数除法被除数小于除数

使用加减交替法时，若第一个商为 1，即被除数更大，将直接停止计算

补码除法——加减交替法

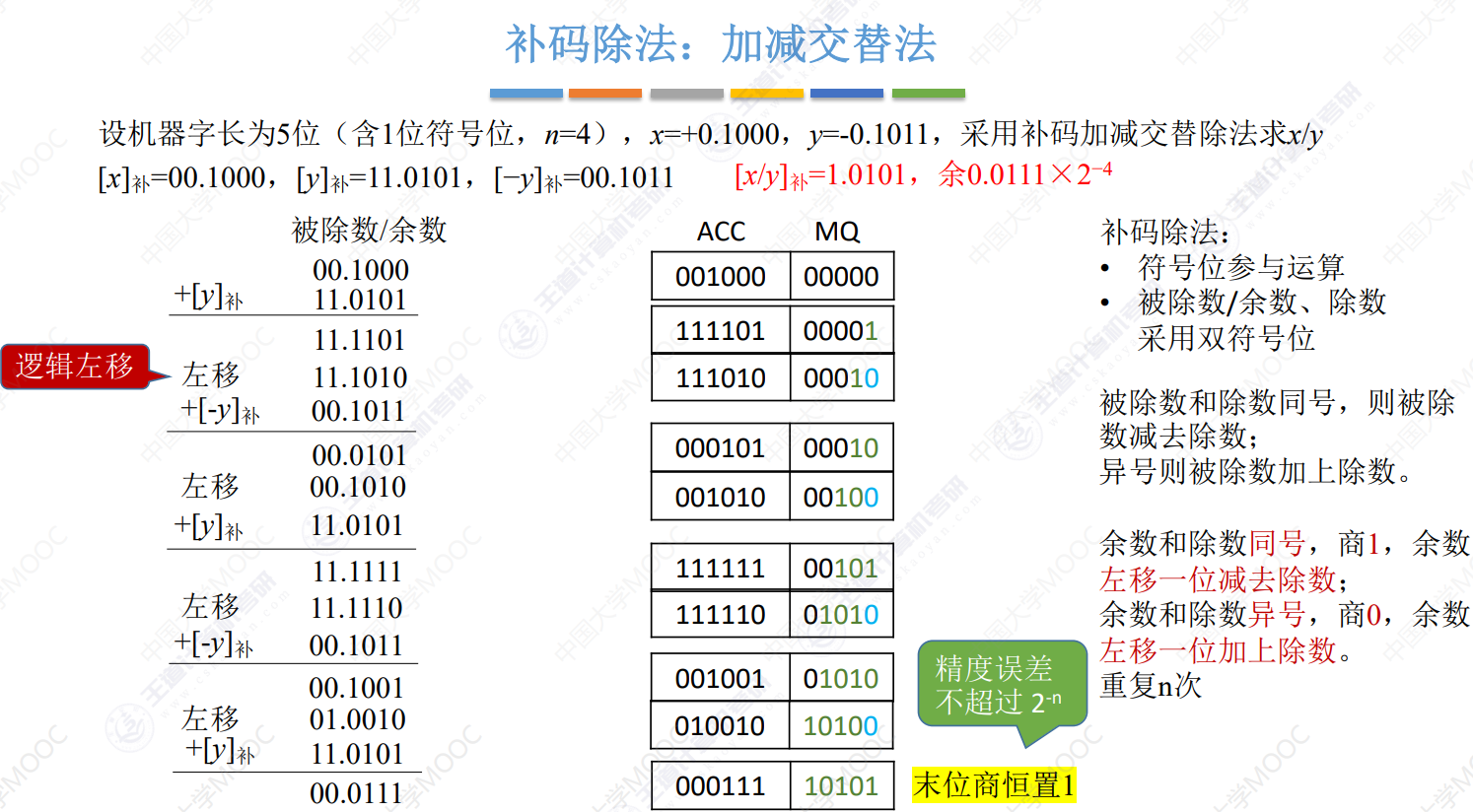
​image​

浮点数的表示和运算

分为一般浮点数和IEEE浮点数

浮点数的表示

浮点数的表示

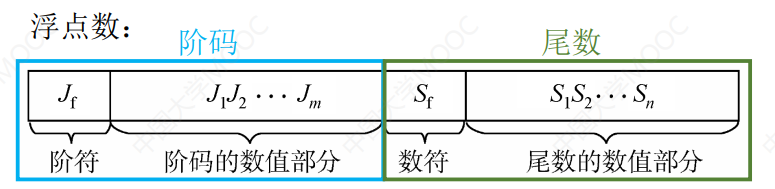
​image​

${\color{Red} 0} ,{\color{Brown} 01} ; {\color{orange} 1 } .{\color{Green} 1001}$

${\color{Red} 阶符 } \ {\color{Brown} 阶码数值} \ {\color{Orange} 数符} \ {\color{Green} 尾数数值}$

小数点位移方向 整数 正负号 小数

  • 阶码

    定点整数（补码/移码）

    反映浮点数表示范围，小数点位置

    • 阶符

      小数点的移动方向

      0 + 尾数算术左移

  • 尾数

    定点小数(原码/补码)

    位数反映浮点数精度

    • 数符

      浮点数的正负

3.026×10+11 记为 +11 +3.026
-3.026×10-5 记为 -5 -3.026

对于二进制补码表示的浮点数

真值-0.111=-1.11×2+1 记为 0,01 ; 1.1001

阶码 0,01 真值 +1
尾数 1.1001 真值 -0.0111

-0.0111 算术左移1位-> -0.111

基数：表示浮点数进制
基数即3.026×10+11中的10，隐含

浮点数规格化

规定尾数最高数值位必须为有效值（不为 0）即有效位尽可能靠近符号位

  • 左规

    运算结果非规格化时，尾数算术左移一位，阶码-1，直到规格化

  • 右规

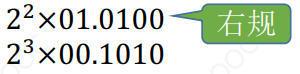
    ​image​

    计算结果发生溢出时挽救溢出（采用双符号位时可挽救溢出）

    尾数右移一位，阶码 +1

  • 规格化快速判断

    只判断尾数，阶码只影响基数上的幂次

    • 原码尾数

      尾数最高位一定为 1

    • 补码尾数

      符号位与最高位数值相反

      注意补码算术移位规则

​image​

对于补码 0,10；0.0100 1

阶码 +2
尾数 +.01001，首位为 0，浪费一位空间

对尾数算术左移一位（左规）0,01；0.1001
此时浮点数数值不变，后者更少的位数表示

对于负数补码，其尾数如1.0100 1，此时最高位0是有效位，最高位若为1无效

见原码转补码规则（数值取反+1）

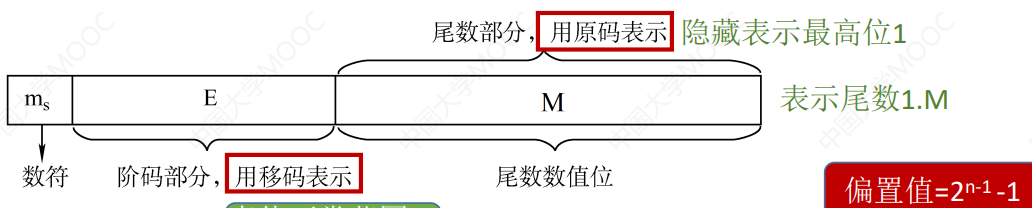
IEEE754 浮点数

  • 注意

    • 数符最前，阶码使用​移码 ，尾数使用​原码
    • 默认为​规约数（默认首位1且隐含）
    • 阶码=真值+偏移量
    • 取 2n-1-1 偏置值时，全 1 与全 0 阶码为特殊阶码
    • 短浮点数的真值：$(-1)^s\times1.M\times2^{E-127}$

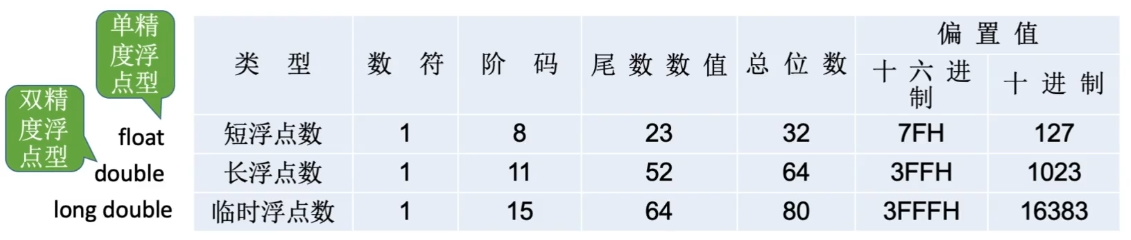
​image​

​image​

​image​

(-0.75)​10​转 IEEE754 单精度浮点数

(-0.75)10 =转二进制= (-0.11)2 =规格化= (-1.1)2×2-1

数符=1
尾数=.10000….(首位 1 隐含)
阶码真值=-1
偏移量=127

阶码移码=阶码真值 + 偏移量 = -1 + 0111 1111 = 0111 1110
或=-1+127=126=0111 1110

即 1 01111110 100000…

IEEE754 单精度浮点数 CO A0 00 00 H 转十进制

CO A0 00 00 H =转二进制= 1 1000000 | .101000……

数符：1=-
阶码真值=移码机器数-偏移量=129-127=(2)10（可将尾数算术左移2位后​直接取整数部分快速判断​）
尾数：(1.01)2=(1.25)10（不要遗漏隐含1）

浮点数真值= (-1.01)2 × 22 = -1.25 × 22 = - 5.0

特殊阶码

  1. 阶码全0

    1. 尾数全0
      由符号位决定+0或-0
    2. 尾数不全0
      非规约数，IEEE标准中的表示尾数0~1内的浮点数

  2. 阶码全1

    1. 尾数全0
      符号位决定+∞或-∞
    2. 尾数不全0 NaN（Not a Number，非数值）
各类范围及数值
形式 阶码 尾数
零 0 0
非规约 0 0<=x<1
规约 1~2E-1 1<=x<2
无穷 2E-1 0
NaN 2E-1 !0
类别 正负号 实际指数 偏置后阶码 阶码域 尾数域 数值
0 0 -127 0 0000 0000 000 0000 0000 0000 0000 0000 +0.0
-0 1 -127 0 0000 0000 000 0000 0000 0000 0000 0000 -0.0
1 0 0 127 0111 1111 000 0000 0000 0000 0000 0000 +1.0
-1 1 0 127 0111 1111 000 0000 0000 0000 0000 0000 -1.0
最小规约数 绝对值 -126 1 0000 0001 000 0000 0000 0000 0000 0000 $1.0\times2^{1-127}=1.0\times2^{-126}$​
最大规约数（1.11111..1=2-2^(-23)使用等比数列求和公式即可得到） 绝对值 127 254 1111 1110 111 1111 1111 1111 1111 1111 $1.11…1\times2^{254-127}=(2-2^{-23})\times2^{127}$​
类别 正负号 实际指数 偏置后阶码 阶码域 尾数域 数值
+∞ 0 128 255 1111 1111 000 0000 0000 0000 0000 0000 +∞
-∞ 1 128 255 1111 1111 000 0000 0000 0000 0000 0000 -∞
NaN —— 128 255 1111 1111 非全 0 NaN
类别 正负号 实际指数 偏置后阶码 阶码域 尾数域 数值
最小非规约数 绝对值 -126 0 0000 0000 000 0000 0000 0000 0000 0001 $0.000…1\times2^{0-126}=2^{-23}\times2^{-126}$​
中间非规约数 绝对值
 -126 0 0000 0000 100 0000 0000 0000 0000 0000 $2^{-1}\times2^{-126}$​
最大非规约数 绝对值 -126 0 0000 0000 111 1111 1111 1111 1111 1111 $0.111…1\times2^{0-126}=(1-2^{-23})\times2^{-126}$​

浮点数的运算

加减运算

  1. 转换

    注意阶码和尾数的表示码

  2. 对阶

    小阶转大阶（算术右移）

  3. 尾数加减

    双符号位表示尾数，挽救尾数溢出

  4. 规格化

  5. 舍入

    • 0 舍 1 入法

      溢出 0，舍去
      溢出 1，尾数末位 +1，若又溢出，则继续右规

    • 恒置 1 法

      使右移后尾数末尾恒为 1

  6. 判断溢出

    规格化后，若阶码上溢，异常，下溢视为机器 0

通常不会直接使用 IEEE754 标准，也即无首位隐含

十进制数 X=-5/256、Y=+59/1024，补码运算 X-Y 阶符 2 位，阶码 3 位，数符 2 位，尾数 9 位

  1. 转换

    X：-(5 × 1/256) -> -(101 × 2-8) -> -(0.101 × 2-5) -> -(0.101 × 2​-101​) -> 11.011;11.011000000

    Y：+(59 × 1/1024) -> +(111011 × 2-10) -> +(0.111011 × 2-4) -> +(0.111011 × 2​-100​) -> 11.100;00.111011000

  2. 对阶

    X：-(0.101 × 2-101) -> -(0.0101 × 2-100) -> 11.100;11.101100000

    Y：+(0.111011 × 2-100) -> 11.100;00.111011000

  3. 尾数加减

    Y： 11.100;00.111011000 -Y：11.100;11.000101000

    X+(-Y)= 11.100;11.101100000

    • 11.100;11.000101000 = 11.100;(1)10.110001000 括号溢出 1

  4. 规格化

    11.100;(1)10.110001000 右规 1 位

    11.101;11.011000100

  5. 舍入

  6. 判断溢出

强制类型转换

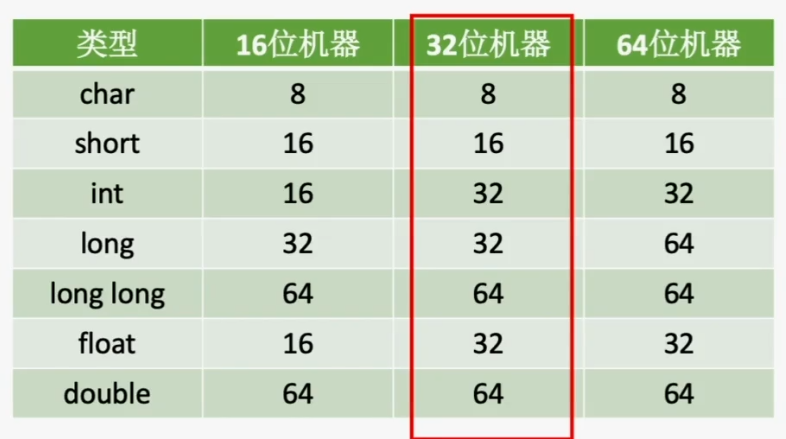
​image​

其他要点

  1. 32位机器中，int转double的加减法无论如何都不会溢出
  2. IEEE754小数部分使用原码！！！！！！
  3. double可以精确表示int
  4. double 0/0得到的结果将是NaN或者崩溃
  5. 遇到类似$2^7 \times \frac{29}{32}$类似浮点数，分母若为2的倍数可视为对分子移位

‍